Advertisements
Advertisements
प्रश्न
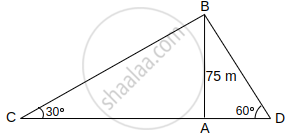
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
उत्तर

In ΔBAD,
tan 60° = `("AB")/("AD")`
⇒ `sqrt(3) = 75/("AD")`
⇒ AD = `75/sqrt(3) xx sqrt(3)/sqrt(3)`
= `(75sqrt(3))/3`
= `25sqrt(3)` m ...(i)
and In ΔBAC,
tan 30° = `("AB")/("AC")`
⇒ `1/sqrt(3) = 75/("AC")`
⇒ AC = `75sqrt(3)` m ...(ii)
From equations (i) and (ii), we have
DC = AC + AD
= `75sqrt(3) + 25sqrt(3)`
= `100sqrt(3)`
= 100 × 1.732
= 173.2 m
Which is the required distance between two men.
संबंधित प्रश्न
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
