Advertisements
Advertisements
प्रश्न
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
उत्तर
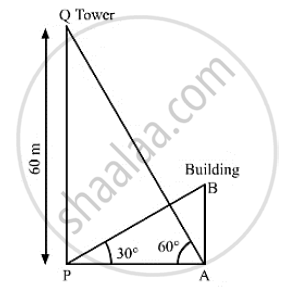
Let AB be thee building and PQ be the tower.
We have,
PQ = 60m,∠APB = 30°, ∠PAQ = 60°
In ΔAPQ,
` tan 60° = (PQ)/(AP)`
`⇒ sqrt(3) = 60/(AP)`
`⇒ AP = 60/sqrt(3)`
`⇒ AP = (60 sqrt(3))/3`
`⇒ AP = 20 sqrt(3) m`
Now , in Δ ABP ,
` tan 30° = (AB)/(AP)`
`⇒1/ sqrt(3) = (AB)/(20 sqrt(3))`
`⇒ AB = (20 sqrt(3))/ sqrt(3)`
∴ AB = 20 m
So, the height of the building is 20 m
APPEARS IN
संबंधित प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
