Advertisements
Advertisements
प्रश्न
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
उत्तर १

Let AB be the building of height 20 m and BC the transmission tower of height h meter.
∴ AB = 20 m
∴ BC = h m
O is the point of observation.
Let the angle of elevation of the bottom and top of the tower at the point o is 45° and 60° respectively.
∴ ∠COA = 60° and ∠BOA = 45°
In ΔOAB,
tan∠BOA = `"AB"/"AO"`
∴ tan 45° = `20/x`
∴ 1 = `20/x`
∴ x = 20 m
∴ AO = 20 m ...(1)
In ΔOAC,
tan ∠COA = `"AC"/"AO"`
tan 60° = `"AB + BC"/"AO"`
`sqrt3 = (20 + h)/20`
20`sqrt3` = 20 + h
∴ h = 20`sqrt3` − 20
∴ h = 20(`sqrt3` − 1)
Here, `sqrt3` = 1.73 ...(Given)
∴ h = 20(1.73 − 1)
∴ h = 20 × 0.73
∴ h = 14.64 m
Height of tower (h) = 14.64 m.
उत्तर २

Let AB be the building of height 20 m and BC the transmission tower of height h meter.
∴ AB = 20 m
∴ BC = h m
O is the point of observation. Let the angle of elevation of the bottom and top of the tower at the point o be 45° and 60°, respectively.
∴ ∠COA = 60° and ∠BOA = 45°
In ΔOAB,
tan∠BOA = `"AB"/"AO"`
∴ tan 45° = `20/x`
∴ 1 = `20/x`
∴ x = 20 m
∴ AO = 20 m ...(1)
In ΔOAC,
tan ∠COA = `"AC"/"AO"`
tan 60° = `"AB + BC"/"AO"`
`sqrt3 = (20 + h)/20`
20`sqrt3` = 20 + h
∴ h = 20`sqrt3` − 20
∴ h = 20(`sqrt3` − 1)
h = 20 × 0.732
h = 14.64
Thus, the height of the tower is 14.64 m.
APPEARS IN
संबंधित प्रश्न
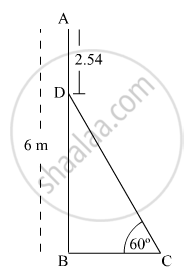
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
