Advertisements
Advertisements
प्रश्न
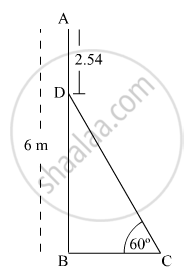
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
उत्तर
In the given figure,
AB = AD + DB = 6 m
Given: AD = 2.54 m
⇒ 2.54 m + DB = 6 m
⇒ DB = 3.46 m
Now, in the right triangle BCD,
`(BD)/(CD)=sin 60^@`
`=>(3.46m)/(CD)=sqrt3/2`
`=>(3.46m)/(CD)=1.73/2`
`=>CD=(2xx3.46m)/1.73`
⇒CD=4 m
Thus, the length of the ladder CD is 4 m.
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
The angle of elevation of the top of a 30 m high tower at a point 30 m away from the base of the tower is ______.
