Question

There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.

Answer 1

Let AB and CE are two temples each at the bank of the river. The top of the temple CE makes an angle of depressions at the top and bottom of tower AB are 30° and 60°

Let CE = 50 m and AB = H m and ∠CBE = 60°, ∠DAE = 30°

The corresponding figure is as follows

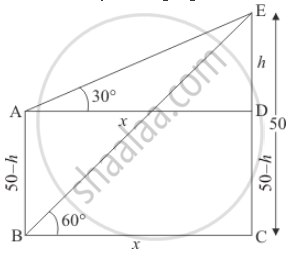
In Δ ADE

`=> tan 30^@ = h/x`

`=> 1/sqrt3 = h/x`

`=> x = hsqrt3`

Again in ΔBCE

`=> tan 60^@ = 50/x`

`=> sqrt3 = 50/x`

`=> 50 = sqrt3 xxx hsqrt3`

`=> h = 50/3`

Now the distance between the temples

`x = hsqrt3`

`= 50/3xx sqrt3`

`= 50/3`

Therefore `H = 50 - 50/3`

`=> H =  33.33

Hence distance between the temples is `50/sqrt3 m = 28.83 m` and height of temple is  33.33 m