Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
उत्तर
Let angle of elevation of an aeroplane is 45°. After 15 seconds angle of elevation is the change to 30°. Let DE be the height of aeroplane which is 3000 meters above the ground.
Let AB = x,BD = y, ∠CAB = 45° and ∠EAD = 30°
Here we have to find speed of aero plane.
We have the corresponding figure as follows
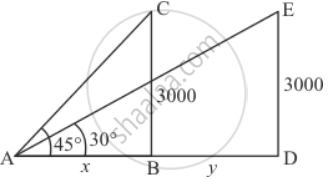
So we use trigonometric ratios.
In Δ ABC
`=> tan A = (BC)/(AB)`
`=> tan 45^@ = 3000/x`
`=> 1 = 3000/x`
`=> x = 3000`
Again in ΔADE
`=> tan A = (DE)/(AB + BD)`
`=> tan 30^@ = 3000/(x + y)`
`=> 1/sqrt3 = 3000/(3000 + y)`
`=> 3000 + y = 3000sqrt3`
`=> y = 3000sqrt3 - 3000`
`=> y = 3000(sqrt3 - 1)`
=> y = 2196
Since 15 sec = 2196
`=> sec = 2196/15 = 146.4`
`= (146.4 xx 3600)/1000`
= 527.04
Hence the speed of aero plane is 527.04 km/h
APPEARS IN
संबंधित प्रश्न
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
