Advertisements
Advertisements
प्रश्न
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
उत्तर
Let h be the height of lighthouse AC. And an angle of depression of the top of the lighthouse from two ships is α and β respectively.
Let BC = x, CD = y. And ∠ABC = α, ∠ADC = β.
We have to find the distance between the ships
We have the corresponding figure as follows
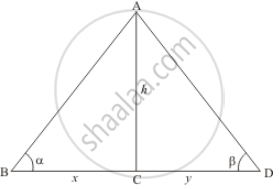
We use trigonometric ratios.
In ΔABC
`=> tan α = (AC)/(BC)`
`=> tan α = h/x`
Again in Δ ADC
`=> tan β = (AC)/(CD)`
`=> tan β = h/y`
`=> y = h/(tan β)`
Now
`=> BD = x + y`
`=> BD = h/(tan α) + h/(tan β)`
`=> BD = (h(tan α + tan β))/(tan α tan β)`
Hence the distance between ships is `(h(tan α + tan β))/(tan α tan β)`
APPEARS IN
संबंधित प्रश्न
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
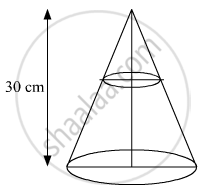
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
The tops of two towers of height x and y, standing on level ground, subtend angles of 30º and 60º respectively at the centre of the line joining their feet, then find x : y.
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
