Advertisements
Advertisements
प्रश्न
The tops of two towers of height x and y, standing on level ground, subtend angles of 30º and 60º respectively at the centre of the line joining their feet, then find x : y.
उत्तर
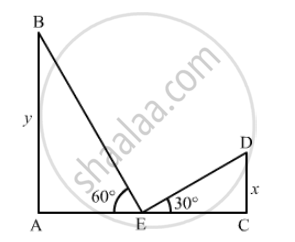
Let AB and CD be the two towers and E be the mid-point of AC.
Height of the tower, AB = y
Height of the tower, CD = x
it is given that, ∠ AEB=60° and ∠ CED=30°
Also, `AE=EC`
In right Δ AEB,
`tan 60°= (AB)/(AE)`
⇒ `sqrt3=y/(AE)`
`⇒ AE=y/sqrt3`
In right ∆CED,
`tan 60° = (AB)/(AF)`
⇒ `1/sqrt3=x/(CE)`
`⇒CE=sqrt3x`
`y/sqrtx=sqrt3x`
`⇒ y=3x`
`⇒x/y=1/3`
`∴ x: y=1:3`
Hence, the ratio of x : y is 1 : 3.
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
