Advertisements
Advertisements
प्रश्न
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
उत्तर
Let h be the height of lighthouse AC. And an angle of depression of the top of the lighthouse from two ships is α and β respectively.
Let BC = x, CD = y. And ∠ABC = α, ∠ADC = β.
We have to find the distance between the ships
We have the corresponding figure as follows
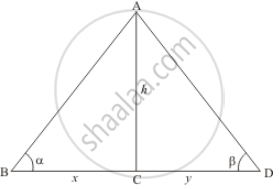
We use trigonometric ratios.
In ΔABC
`=> tan α = (AC)/(BC)`
`=> tan α = h/x`
Again in Δ ADC
`=> tan β = (AC)/(CD)`
`=> tan β = h/y`
`=> y = h/(tan β)`
Now
`=> BD = x + y`
`=> BD = h/(tan α) + h/(tan β)`
`=> BD = (h(tan α + tan β))/(tan α tan β)`
Hence the distance between ships is `(h(tan α + tan β))/(tan α tan β)`
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
