Advertisements
Advertisements
प्रश्न
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
उत्तर
Let AB be the height of tower 50 m and angle of depression from the top of the tower are 60° and 30° respectively at two observing Car C and D.
Let BD = x m, CD = y m and ∠ADB = 30°, ∠ACb = 60°
We have the corresponding figure as follows
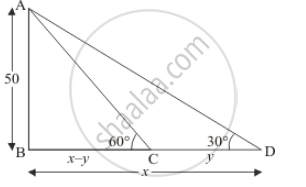
So we use trigonometric ratios.
In a triangle ABD
`=> tan D = (AB)/(BD)`
`=> tan 30° = 50/x`
`=> 1/sqrt3 = 50/x`
`=> x = 50sqrt3`
Since x = 86.6
Again in a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60° = 50/(x - y)`
`=> sqrt3 = 50/(x - y)`
`=> sqrtt3 xx 50sqrt3 - sqrt3y = 50`
`=> y = 57.67`
Therefore x - y= 86.6 - 57.67
`=> x - y = 28.93`
Hence the distance of first car from tower is 86.6 m
And the distance of second car from tower is 57.67 m
And the distance between cars is 28.93 m
APPEARS IN
संबंधित प्रश्न
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
