Advertisements
Advertisements
Question
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
Solution
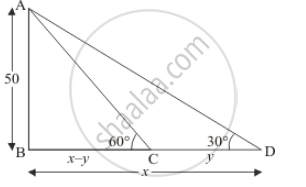
Let AB be the height of tower 50 m and angle of depression from the top of the tower are 60° and 30° respectively at two observing Car C and D.
Let BD = x m, CD = y m and ∠ADB = 30°, ∠ACb = 60°
We have the corresponding figure as follows
So we use trigonometric ratios.
In a triangle ABD
`=> tan D = (AB)/(BD)`
`=> tan 30° = 50/x`
`=> 1/sqrt3 = 50/x`
`=> x = 50sqrt3`
Since x = 86.6
Again in a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60° = 50/(x - y)`
`=> sqrt3 = 50/(x - y)`
`=> sqrtt3 xx 50sqrt3 - sqrt3y = 50`
`=> y = 57.67`
Therefore x - y= 86.6 - 57.67
`=> x - y = 28.93`
Hence the distance of first car from tower is 86.6 m
And the distance of second car from tower is 57.67 m
And the distance between cars is 28.93 m
APPEARS IN
RELATED QUESTIONS
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
The distance of point A(-5, 6) from the origin is ______.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
