Advertisements
Advertisements
Question
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
Solution
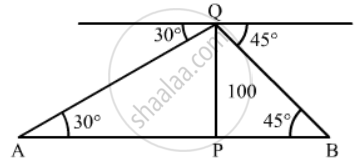
Let PQ be the tower and A and B are two cars.
We have,
PQ = 100 m, ∠PAQ = 30° and ∠PBQ = 45°
In ∆APQ
`tan 30^@ = (PQ)/(AP)`
`=> 1/sqrt3 = 100/(AP)`
`=> AP =100sqrt3` m
Also In ∆ BPQ
`tan 45^@ = (PQ)/(BP)`
`=> 1= 100/(BP)`
`=> BP = 100 m`
Now, AB = AP + BP`
`= 100sqrt3 + 100`
`=100(sqrt3 + 1)`
=100 x (1.732 + 1)
= 100 x 2.732
= 273.2 m
So the distance between the cars is 273.2 m
APPEARS IN
RELATED QUESTIONS
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
|
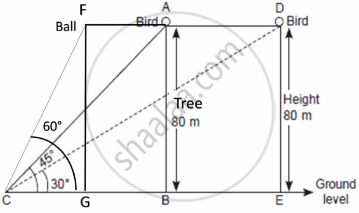
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?