Advertisements
Advertisements
Question
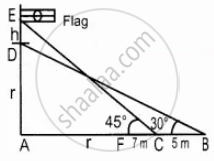
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

Solution
Height of the Flag pole (ED) = h m
AF and AD is the radius of the semi circle (r)
AC = (r + 7)
AB = (r + 7 + 5)
= (r + 12)
In the right ∆ABD, tan 30° = `"AD"/"AB"`
`1/sqrt(3) = r/("r" + 12)`
`sqrt(3` r = r + 12
`sqrt(3)` r − r = 12
⇒ `"r" (sqrt(3) - 1)` = 12
r[1.732 – 1] = 12
⇒ 0.732r = 12
r = `12/(0.732)` ⇒ = 16.39 m
In the right ∆ACE, tan 45° = `"AE"/"AC"`
`1 + ("r" + "h")/("r" + 7)`
r + 7 = r + h
∴ h = 7 m
Height of the pole (h) = 7 m
APPEARS IN
RELATED QUESTIONS
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
