Advertisements
Advertisements
प्रश्न
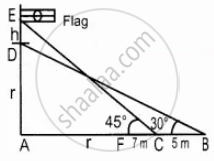
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

उत्तर
Height of the Flag pole (ED) = h m
AF and AD is the radius of the semi circle (r)
AC = (r + 7)
AB = (r + 7 + 5)
= (r + 12)
In the right ∆ABD, tan 30° = `"AD"/"AB"`
`1/sqrt(3) = r/("r" + 12)`
`sqrt(3` r = r + 12
`sqrt(3)` r − r = 12
⇒ `"r" (sqrt(3) - 1)` = 12
r[1.732 – 1] = 12
⇒ 0.732r = 12
r = `12/(0.732)` ⇒ = 16.39 m
In the right ∆ACE, tan 45° = `"AE"/"AC"`
`1 + ("r" + "h")/("r" + 7)`
r + 7 = r + h
∴ h = 7 m
Height of the pole (h) = 7 m
APPEARS IN
संबंधित प्रश्न
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
In figure given ABCD is a rectangle, the value of CE is ____________.

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
