Advertisements
Advertisements
प्रश्न
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
उत्तर
Let BD be the width of the river. And the angle of depression of the bank on opposite side of the river is 30° and 45° respectively. It is given that AC = 30 m.
Let BC = x and CD = y. And ∠ABC = 30°, ∠ADC = 45°.
Here we have to find the width of the river.
We have the following figure
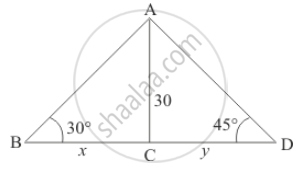
So we use trigonometric ratios.
In a triangle ABC
`=> tan 30° = (AC)/(BC)`
`=> 1/sqrt3 = 30/x`
`=> x = 30sqrt3`
Again in a triangle ADC
`=> tan 45° = (AC)/(CD)`
`=> 1 = 30/y`
`=> y = 30`
So width of river is
`x + y = 30sqrt3`
`x + y = 30(sqrt3 + 1)`
Hence the width of river is `(30(sqrt3 + 1)`m
APPEARS IN
संबंधित प्रश्न
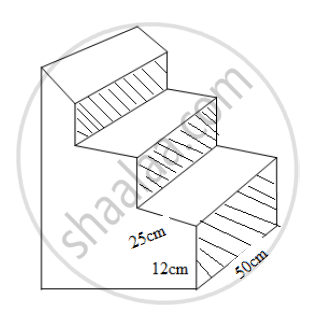
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
