Advertisements
Advertisements
प्रश्न
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
उत्तर
Let BD be the width of the river. And the angle of depression of the bank on opposite side of the river is 30° and 45° respectively. It is given that AC = 30 m.
Let BC = x and CD = y. And ∠ABC = 30°, ∠ADC = 45°.
Here we have to find the width of the river.
We have the following figure
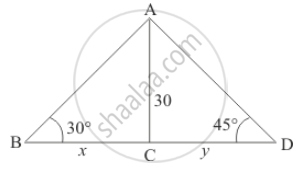
So we use trigonometric ratios.
In a triangle ABC
`=> tan 30° = (AC)/(BC)`
`=> 1/sqrt3 = 30/x`
`=> x = 30sqrt3`
Again in a triangle ADC
`=> tan 45° = (AC)/(CD)`
`=> 1 = 30/y`
`=> y = 30`
So width of river is
`x + y = 30sqrt3`
`x + y = 30(sqrt3 + 1)`
Hence the width of river is `(30(sqrt3 + 1)`m
APPEARS IN
संबंधित प्रश्न
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
