Advertisements
Advertisements
प्रश्न
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
उत्तर
Let the height of the lamp post AE be h m
DE = h – 66
Let AB be x
In the right ∆ABC, tan 30° = `"BC"/"AB"`
`1/sqrt(3) = 66/x`
x = `66sqrt(3)` ...(1)
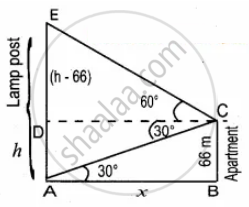
In the right ∆CDE, tan 60° = `"DE"/"DC"`
`sqrt(3) = ("h" - 66)/x`
⇒ `sqrt(3)x` = h – 66
x = `("h" - 66)/sqrt(3)` ...(2)
From (1) and (2) we get
`("h" - 66)/sqrt(3) = 66sqrt(3)`
h – 66 = `66sqrt(3) xx sqrt(3)` = 66 × 3
h – 66 = 198 ⇒ h = 198 + 66
h = 264 m
Distance between the lamp post and the apartment
= `66 sqrt(3)` m
= 66 × 1.732
= 114.31 m
APPEARS IN
संबंधित प्रश्न
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

