Advertisements
Advertisements
प्रश्न
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
उत्तर
Let the height of the lamp post AE be h m
DE = h – 66
Let AB be x
In the right ∆ABC, tan 30° = `"BC"/"AB"`
`1/sqrt(3) = 66/x`
x = `66sqrt(3)` ...(1)
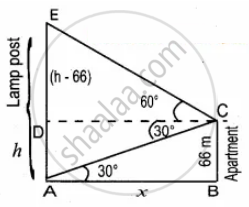
In the right ∆CDE, tan 60° = `"DE"/"DC"`
`sqrt(3) = ("h" - 66)/x`
⇒ `sqrt(3)x` = h – 66
x = `("h" - 66)/sqrt(3)` ...(2)
From (1) and (2) we get
`("h" - 66)/sqrt(3) = 66sqrt(3)`
h – 66 = `66sqrt(3) xx sqrt(3)` = 66 × 3
h – 66 = 198 ⇒ h = 198 + 66
h = 264 m
Distance between the lamp post and the apartment
= `66 sqrt(3)` m
= 66 × 1.732
= 114.31 m
APPEARS IN
संबंधित प्रश्न
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
