Advertisements
Advertisements
प्रश्न
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
उत्तर १
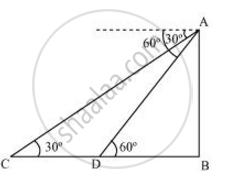
Let AB be the tower.
Initial position of the car is C, which changes to D after six seconds.
In ΔADB,
`("AB")/("DB") = tan 60º`
`("AB")/("DB") =sqrt3`
`"DB" = ("AB")/sqrt3`
In ΔABC,
`("AB")/("BC") = tan 30º`
`("AB")/("BD" + "DC") = 1/sqrt3`
`"AB"sqrt3 = "BD" + "DC"`
`"AB"sqrt3 = ("AB")/sqrt3 + "DC"`
`"DC" = "AB"sqrt3 - ("AB")/sqrt3 = "AB"(sqrt3 - 1/sqrt3)`
= `(2"AB")/sqrt3`
Time taken by the car to travel distance DC `("i.e" "2AB"/sqrt3)` = 6 second
Time taken by the car to travel distance DB `("i.e" ("AB")/sqrt3) = 6/((2"AB")/sqrt3)xx("AB")/sqrt3`
= `6/2`
= 3 seconds
उत्तर २
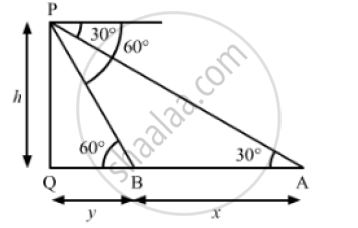
Let PQ be the tower.
We have,
∠PBQ = 60° and ∠PAQ = 30°
Let PQ = h, AB = x and BQ = y
In ΔAPQ,
`tan 30° = (PQ)/(AQ)`
⇒ `1/ sqrt(3) = h/(x+y) `
⇒ `x+y = h sqrt(3)` ...(1)
Also, in ΔBPQ,
`tan 60° = (PQ)/(BQ)`
⇒ `sqrt(3) = h/y`
⇒ `h = y sqrt(3) ` ...(2)
Substituting `h = y sqrt(3)` in (i), we get
`x +y = sqrt(3) (ysqrt(3))`
⇒ x + y = 3y
⇒ 3y - y = x
⇒ 2y = x
⇒ `y = x/2`
`"As, speed of the car from "A to B = (AB) /6 = x/6 "units"/ "sec"`
So, the time taken to reach the foot of the tower i.e. Q from B `(BQ)/(speed)`
= `y/((x/6))`
= `((x/2))/((x/6))`
= `6/2`
= 3 sec
So, the time taken to reach the foot of the tower from the given point is 3 seconds.
संबंधित प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
Find the angle of elevation of the sun when the shadow of a pole h metres high is `sqrt(3)` h metres long.
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
