Advertisements
Advertisements
Question
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution 1
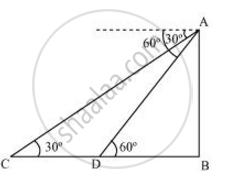
Let AB be the tower.
Initial position of the car is C, which changes to D after six seconds.
In ΔADB,
`("AB")/("DB") = tan 60º`
`("AB")/("DB") =sqrt3`
`"DB" = ("AB")/sqrt3`
In ΔABC,
`("AB")/("BC") = tan 30º`
`("AB")/("BD" + "DC") = 1/sqrt3`
`"AB"sqrt3 = "BD" + "DC"`
`"AB"sqrt3 = ("AB")/sqrt3 + "DC"`
`"DC" = "AB"sqrt3 - ("AB")/sqrt3 = "AB"(sqrt3 - 1/sqrt3)`
= `(2"AB")/sqrt3`
Time taken by the car to travel distance DC `("i.e" "2AB"/sqrt3)` = 6 second
Time taken by the car to travel distance DB `("i.e" ("AB")/sqrt3) = 6/((2"AB")/sqrt3)xx("AB")/sqrt3`
= `6/2`
= 3 seconds
Solution 2
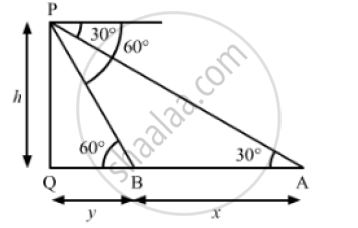
Let PQ be the tower.
We have,
∠PBQ = 60° and ∠PAQ = 30°
Let PQ = h, AB = x and BQ = y
In ΔAPQ,
`tan 30° = (PQ)/(AQ)`
⇒ `1/ sqrt(3) = h/(x+y) `
⇒ `x+y = h sqrt(3)` ...(1)
Also, in ΔBPQ,
`tan 60° = (PQ)/(BQ)`
⇒ `sqrt(3) = h/y`
⇒ `h = y sqrt(3) ` ...(2)
Substituting `h = y sqrt(3)` in (i), we get
`x +y = sqrt(3) (ysqrt(3))`
⇒ x + y = 3y
⇒ 3y - y = x
⇒ 2y = x
⇒ `y = x/2`
`"As, speed of the car from "A to B = (AB) /6 = x/6 "units"/ "sec"`
So, the time taken to reach the foot of the tower i.e. Q from B `(BQ)/(speed)`
= `y/((x/6))`
= `((x/2))/((x/6))`
= `6/2`
= 3 sec
So, the time taken to reach the foot of the tower from the given point is 3 seconds.
RELATED QUESTIONS
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
In given figure, ABCD is a || gm. The length of AP is ____________.
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
