Advertisements
Advertisements
Question
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
Solution
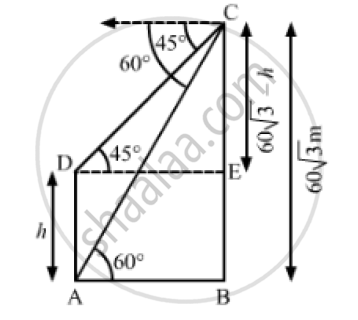
Let AD be the tower and BC be the cliff.
We have,
BC = 60 `sqrt(3)` , ∠ CDE = 45° and ∠BAC = 60°
Let AD = h
⇒ BE = AD = h
⇒ CE = BC - BE= 60 `sqrt(3)` - h
In ΔCDE,
` tan 45° = (CE)/(DE)`
`⇒ 1 = (60 sqrt(3) -h)/(DE)`
`⇒ DE = 60 sqrt(3) - h`
`⇒ AB = DE = 60 sqrt(3) - h` ............(1)
Now, in ΔABC
`tan 60° = (BC)/(AB)`
`⇒ sqrt(3)= (60 sqrt(3) )/ (60 sqrt(3) -h)` [ Using (1)]
`⇒ 180 - h sqrt(3) = 60 sqrt(3)`
`⇒ h sqrt(3) = 180- 60 sqrt(3)`
`⇒ h = (108 -60sqrt(3) )/sqrt(3) xx sqrt(3)/sqrt(3)`
`⇒ h = ( 180 sqrt(3)-180) /3`
`⇒ h = (180 sqrt(3)-1) /3`
∴` h = 60 ( sqrt(3)-1)`
= 60 (1.732 -1)
= 60 (0.7.32)
Also, h = 43.92m
So, the height of the tower is 43. 92 m.
RELATED QUESTIONS
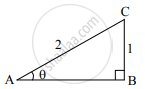
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
