Advertisements
Advertisements
प्रश्न
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
उत्तर
Let the height of the lamp post AE be h m
DE = h – 66
Let AB be x
In the right ∆ABC, tan 30° = `"BC"/"AB"`
`1/sqrt(3) = 66/x`
x = `66sqrt(3)` ...(1)
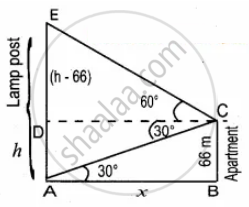
In the right ∆CDE, tan 60° = `"DE"/"DC"`
`sqrt(3) = ("h" - 66)/x`
⇒ `sqrt(3)x` = h – 66
x = `("h" - 66)/sqrt(3)` ...(2)
From (1) and (2) we get
`("h" - 66)/sqrt(3) = 66sqrt(3)`
h – 66 = `66sqrt(3) xx sqrt(3)` = 66 × 3
h – 66 = 198 ⇒ h = 198 + 66
h = 264 m
Difference of the height of lamp post and apartment
= 264 – 66
= 198 m
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
