Advertisements
Advertisements
Question
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
Solution
Let the height of the lamp post AE be h m
DE = h – 66
Let AB be x
In the right ∆ABC, tan 30° = `"BC"/"AB"`
`1/sqrt(3) = 66/x`
x = `66sqrt(3)` ...(1)
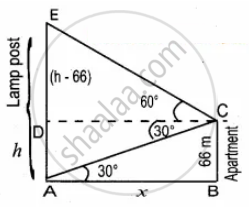
In the right ∆CDE, tan 60° = `"DE"/"DC"`
`sqrt(3) = ("h" - 66)/x`
⇒ `sqrt(3)x` = h – 66
x = `("h" - 66)/sqrt(3)` ...(2)
From (1) and (2) we get
`("h" - 66)/sqrt(3) = 66sqrt(3)`
h – 66 = `66sqrt(3) xx sqrt(3)` = 66 × 3
h – 66 = 198 ⇒ h = 198 + 66
h = 264 m
Difference of the height of lamp post and apartment
= 264 – 66
= 198 m
APPEARS IN
RELATED QUESTIONS
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
