Advertisements
Advertisements
Question
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

Solution
Let AD is the vertical height between A and B
In the right ∆ABD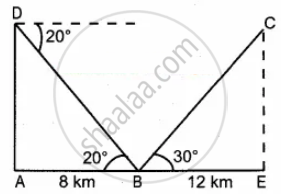
tan 20° = `"AD"/"BD"`
0.3640 = `"AD"/8`
AD = 0.3640 × 8 = 2.912 km
∴ AD = 2.91 km
CE is the vertical height between C and B
In the right ∆BCE, tan 30° = `"CE"/"BE"`
`1/sqrt(3) = "CE"/12`
⇒ `sqrt(3)"CE"` = 12
CE = `12/sqrt(3)`
= `(12 xx sqrt(3))/(sqrt(3) xx sqrt(3))`
= `(12 xx sqrt(3))/3`
= `4sqrt(3)`
= 4 × 1.732
= 6.928
= 6.93 km
The vertical height between A and B = 2.91 km
APPEARS IN
RELATED QUESTIONS
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
In given figure, the length of AP is ____________.

Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
