Advertisements
Advertisements
Question
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
Solution
Let h be the height of light house AC. And an angle of depression of the top of light house from two ships are ∝ and ß respectively. Let` BC=x, CD=y`,. And ∠ABC =∝, ∠ADC=ß , .
We have to find distance between the ships
We have the corresponding figure as follows
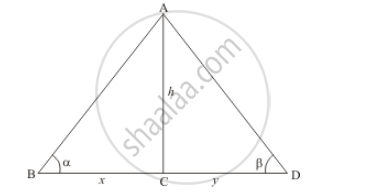
We use trigonometric ratios.
In `Δ ABC`
⇒` tan ∝ =(AC)/(BC)`
⇒` tan ∝= h/x`
⇒` x= h/ tan ∝`
Again in `Δ ADC`
⇒ `tan ß=(AC)/(CD)`
⇒` tan ß= h/y`
⇒` y=h/tan ß`
Now,
⇒ `BD=x+y`
⇒ `BD= h/tan ∝ +h/tan ß`
⇒ `BD= (h(tan∝+tan ß ))/(tan ∝ tanß)`
Hence the distance between ships is `(h(tan∝+tan ß))/(tan∝ tan ß)`
APPEARS IN
RELATED QUESTIONS
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

In given figure, the value of AE is ____________.
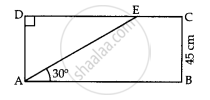
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
