Advertisements
Advertisements
Question
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
Solution

Let the two objects be at points C and D.
The angle of depression for the point C is `ßß` and for the point D is `∝∝`
In ∆ABC,
`tan ß=h/(BC)`
`⇒ BC= h /tanß `
`⇒ tan∝= h/( BC+CD)`
`⇒∝= h/(h/tanß+CD)`
`⇒h/ tanß+CD= h/tan∝`
`⇒ CD= h/tan∝-h/tanß`
`⇒ CD=h [1/tan∝-1/tanß]`
`⇒CD=h [cot ∝-cot ß]`
APPEARS IN
RELATED QUESTIONS
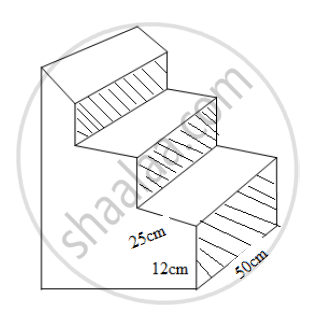
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The Distance of the point (−3, 4) from the x-axis is
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
