Advertisements
Advertisements
प्रश्न
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
उत्तर
Let h be the height of light house AC. And an angle of depression of the top of light house from two ships are ∝ and ß respectively. Let` BC=x, CD=y`,. And ∠ABC =∝, ∠ADC=ß , .
We have to find distance between the ships
We have the corresponding figure as follows
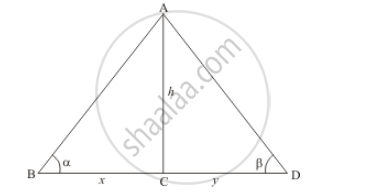
We use trigonometric ratios.
In `Δ ABC`
⇒` tan ∝ =(AC)/(BC)`
⇒` tan ∝= h/x`
⇒` x= h/ tan ∝`
Again in `Δ ADC`
⇒ `tan ß=(AC)/(CD)`
⇒` tan ß= h/y`
⇒` y=h/tan ß`
Now,
⇒ `BD=x+y`
⇒ `BD= h/tan ∝ +h/tan ß`
⇒ `BD= (h(tan∝+tan ß ))/(tan ∝ tanß)`
Hence the distance between ships is `(h(tan∝+tan ß))/(tan∝ tan ß)`
APPEARS IN
संबंधित प्रश्न
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
In Fig. 3, the area of triangle ABC (in sq. units) is:
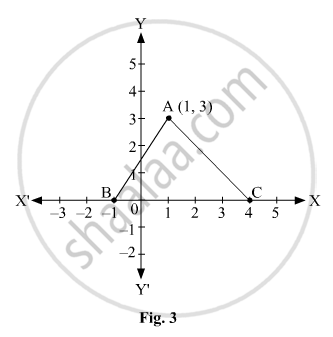
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
