Advertisements
Advertisements
प्रश्न
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
उत्तर
Let AC be the lamp post of height h
We assume that ED = 1.6 m, BE = 4.8 m and EC = 3.2 m
We have to find the height of the lamp post
Now we have to find the height of lamp post using similar triangles.
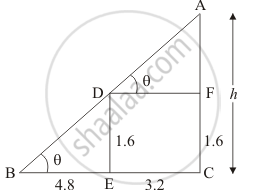
Since triangle BDE and triangle ABC are similar.
`(AC)/(BC) = (ED)/(BE)`
`h/(4.8 + 3.2) = 1.6/(BE)`
`h = 8/3`
Again, we have to find height of lamp post using trigonometric ratios.
In ΔADE
`=> tan theta = 1.6/4.8`
`=> tan theta = 1/3`
Again in ΔABC
`=> tan theta = h/(4.8 + 3.2)`
`=> 1/2 = h/8`
`h = 8/3`
Hence the height of lamp post is 8/3 m
APPEARS IN
संबंधित प्रश्न
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
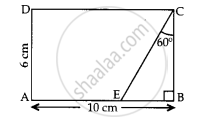
In given figure, the value of CE is ____________.
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
