Advertisements
Advertisements
Question
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
Solution
Let AB be the wall of height, hm and C be the points, makes an angle 60° and foot of the ladder is 2m away from the wall. We have to find the height of the wall
In a triangle ABC, given that BC = 2m and angle C = 60°
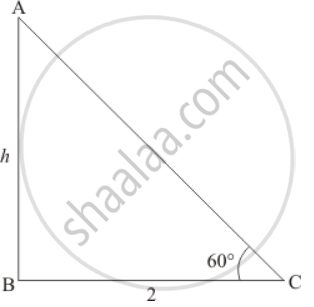
Now we have to find the height of the wall.
So we use trigonometrically ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60^@ = h/2`
`=> sqrt3 = h/2`
`=> h = 2sqrt3`
Hence height of wall is `2sqrt3` meters
APPEARS IN
RELATED QUESTIONS
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
