Advertisements
Advertisements
Question
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
Solution
Let AB be the unfinished tower, AC be the raised tower and O be the point of observation
We have:
OA = 75m,∠AOB = 30° and ∠AOC = 60°
Let AC = H m such that BC = (H -h)m.
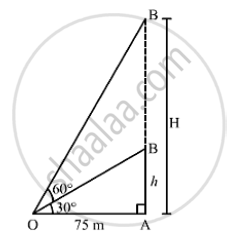
In ΔAOB,we have:
`(AB)/(OA) = tan 30° = 1/ sqrt(3)`
`⇒ h/ 75 = 1/ sqrt(3)`
`⇒ = 75/ sqrt(3) m = (75 xx sqrt(3)) /(sqrt(3) xx sqrt(3)) = 25 sqrt(3) m`
In ΔAOC,we have:
`(AC)/(OA) = tan 60° = sqrt(3)`
`⇒ H/75 = sqrt(3)`
`⇒ H = 75 sqrt(3 )m`
`∴"Required height" =(H - h) = (75 sqrt(3) - 25 sqrt(3)) = 50 sqrt(3)m = 86.6m`
APPEARS IN
RELATED QUESTIONS
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
