Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
उत्तर
Let AB be the unfinished tower, AC be the raised tower and O be the point of observation
We have:
OA = 75m,∠AOB = 30° and ∠AOC = 60°
Let AC = H m such that BC = (H -h)m.
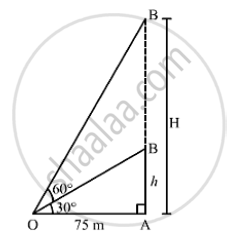
In ΔAOB,we have:
`(AB)/(OA) = tan 30° = 1/ sqrt(3)`
`⇒ h/ 75 = 1/ sqrt(3)`
`⇒ = 75/ sqrt(3) m = (75 xx sqrt(3)) /(sqrt(3) xx sqrt(3)) = 25 sqrt(3) m`
In ΔAOC,we have:
`(AC)/(OA) = tan 60° = sqrt(3)`
`⇒ H/75 = sqrt(3)`
`⇒ H = 75 sqrt(3 )m`
`∴"Required height" =(H - h) = (75 sqrt(3) - 25 sqrt(3)) = 50 sqrt(3)m = 86.6m`
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
