Advertisements
Advertisements
प्रश्न
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
उत्तर
Let AB be the tower of height 150 m and Two objects are located when the top of the tower are observed, makes an angle of depression from the top and bottom of the tower are 45° 60° respectively.
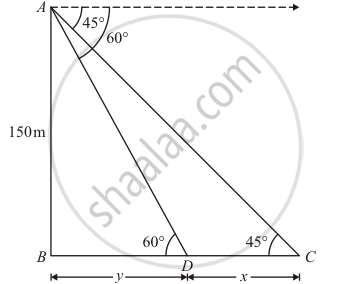
Let CD = x, BD = y, ∠ADB = 60°, ∠ACB = 45°
So we use trigonometric ratios.
In a triangle ABC,
`tan 45^@ = 150/(x + y)`
`=> x = y = 150` ......(1)
Again in a triangle ABD,
`tan 60^@ = 150/y`
`=> sqrt3 = 150/y`
`=> sqrt3 = 150` ......(2)
So from (1) and (2) we get
`x + 150/sqrt3 = 150`
`=> sqrt3x = 150(sqrt3 - 1)`
`=> x = 63.39`
Hence the required distance is approximately 63.4 m
APPEARS IN
संबंधित प्रश्न
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
