Advertisements
Advertisements
प्रश्न
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
उत्तर
Let CD be the hill and suppose the man is standing on the deck of a ship at point A.
The angle of depression of the base C of the hill CD observed from A is 30° and the angle of elevation of the top D of the hill CD observed from A is 60°.
∴ ∠EAD = 60° and ∠BCA = 30°
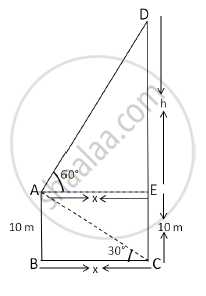
In ΔAED,
tan60° = `(DE)/(EA)`
`:.sqrt3=h/x`
`:.h=sqrt3x `
In ABC
tan30° = `(AB)/(BC)`
`:.1/sqrt3=10/x`
`:.x=10sqrt3 `
Substituting x = 10 `sqrt3` in equation (1) we get
`h=sqrt3xx10sqrt3=10xx3=30`
∴ DE = 30 m
∴ CD = CE + ED = 10 + 30 = 40 m
Thus, the distance of the hill from the ship is `10sqrt3` m and the height of the hill is 40 m
APPEARS IN
संबंधित प्रश्न
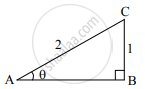
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
