Advertisements
Advertisements
Question
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
Solution
Let CD be the hill and suppose the man is standing on the deck of a ship at point A.
The angle of depression of the base C of the hill CD observed from A is 30° and the angle of elevation of the top D of the hill CD observed from A is 60°.
∴ ∠EAD = 60° and ∠BCA = 30°
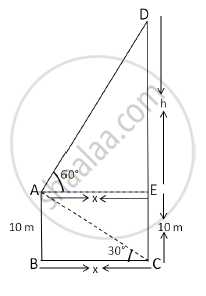
In ΔAED,
tan60° = `(DE)/(EA)`
`:.sqrt3=h/x`
`:.h=sqrt3x `
In ABC
tan30° = `(AB)/(BC)`
`:.1/sqrt3=10/x`
`:.x=10sqrt3 `
Substituting x = 10 `sqrt3` in equation (1) we get
`h=sqrt3xx10sqrt3=10xx3=30`
∴ DE = 30 m
∴ CD = CE + ED = 10 + 30 = 40 m
Thus, the distance of the hill from the ship is `10sqrt3` m and the height of the hill is 40 m
APPEARS IN
RELATED QUESTIONS
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

