Advertisements
Advertisements
Question
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
Options
200 m
500 m
30 m
400 m
Solution
Let AB be the surface of the lake and P be the point of observation. So AP=60 m.
The given situation can be represented as,
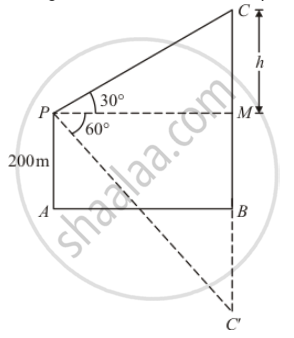
Here,C is the position of the cloud and C' is the reflection in the lake. Then `CB=C'B`.
Let `PM` be the perpendicular from P on CB. Then `∠CPM=30°` and`∠C' PM=60°` and .
Let`CM=h` `PM=x`, , then`CB=h+200` and`C'B=h+200`
Here, we have to find the height of cloud.
So we use trigonometric ratios.
In ,`ΔCMP`
`⇒ tan 30°=CM/PM`
`⇒1/sqrt3=h/x`
`⇒x=sqrt3h`
Again in `ΔPMC`
`⇒ tan 60°= (C'M)/(PM)`
`⇒sqrt3=(C'B+BM)/(PM)`
`⇒sqrt3=(h+200+200)/x`
`⇒ sqrt3x=h+400`
Put `x=sqrt3h`
`⇒3h=h+400`
`⇒ 2h=400`
`⇒h=200`
Now,
`⇒ CB=h+200`
`⇒ CB=200+200`
`⇒ CB=400`
APPEARS IN
RELATED QUESTIONS
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
