Question

On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.

Answer 1

Let AB be the tower of height 150 m and Two objects are located when the top of the tower are observed, makes an angle of depression from the top and bottom of the tower are 45° 60° respectively.

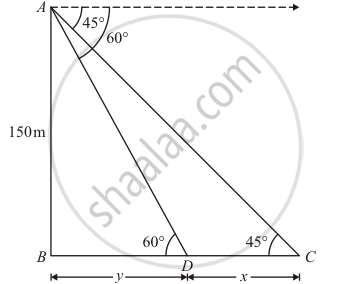
Let CD = x, BD = y, ∠ADB = 60°, ∠ACB = 45°

So we use trigonometric ratios.

In a triangle ABC,

${\displaystyle {\tan 45}^{\circ }=\frac{150}{x+y}}$

${\displaystyle \Rightarrow x=y=150}$   ......(1)

Again in a triangle ABD,

${\displaystyle {\tan 60}^{\circ }=\frac{150}{y}}$

${\displaystyle \Rightarrow \sqrt{3}=\frac{150}{y}}$

${\displaystyle \Rightarrow \sqrt{3}=150}$  ......(2)

So from (1) and (2) we get

${\displaystyle x+\frac{150}{\sqrt{3}}=150}$

${\displaystyle \Rightarrow \sqrt{3}x=150(\sqrt{3}-1)}$

${\displaystyle \Rightarrow x=63.39}$

Hence the required distance is approximately 63.4 m