Advertisements
Advertisements
Question
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
Solution
C and D are the positions of the two boats.
Let the distance between the two boats be “x”
Let BC = y
∴ BD = (x + y)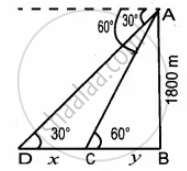
In the right ∆ABC, tan 30° = `"AB"/"BD"`
`1/sqrt(3) = 1800/(x + y)`
x + y = `1800sqrt(3)`
y = `1800sqrt(3) - x` ...(1)
In the right ∆ABC, tan 60° = `"AB"/"BC"`
`sqrt(3) = 1800/y`
y = `1800/sqrt(3)` ...(2)
From (1) and (2) we get
`1800/sqrt(3) = 1800sqrt(3) - x`
1800 = `1800 xx 3 - sqrt(3)x`
`sqrt(3)x` = 5400 – 1800
x = `3600/sqrt(3)`
= `(3600 xx sqrt3)/(sqrt3 xx sqrt(3)`
= `(3600 xx sqrt(3))/3`
= 1200 × 1.732
= 2078.4 m
Distance between the two boats = 2078.4 m
APPEARS IN
RELATED QUESTIONS
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
