Advertisements
Advertisements
Question
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
Solution
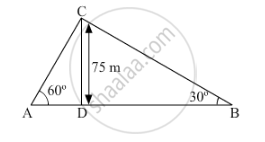
Let CD be the height of the building.
So,
CD = 75 m
It is given that two men are at points A and B and they observe angles of elevation of the top of the building as 60° and 30°, respectively.
\[In ∆ ACD, \]
\[\tan60^o = \frac{CD}{AD}\]
\[ \Rightarrow \sqrt{3} = \frac{75}{AD}\]
\[ \Rightarrow AD = 25\sqrt{3} m\]
\[In ∆ BCD, \]
\[\tan30^o = \frac{CD}{BD}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{75}{BD}\]
\[ \Rightarrow BD = 75\sqrt{3} m\]
∴ Distance between both the men = BD + AD =
APPEARS IN
RELATED QUESTIONS
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
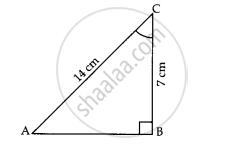
In given figure, the value of ZC is ____________.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
