Advertisements
Advertisements
Question
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
Solution
Let the height of the lamp post be h
The height of the tower (BC) = 60 m
∴ EC = 60 – h
Let AB be x
In the right ∆ABC,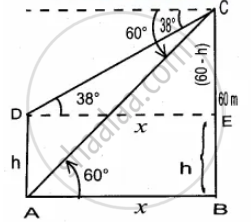
tan 60° = `"BC"/"AB"`
`sqrt(3) = 60/x`
x = `60/sqrt(3)` ...(1)
In the right ∆DEC, tan 38° = `"EC"/"DE"`
0.7813 = `(60 - "h")/x`
x = `(60 - "h")/(0.7813)` ...(2)
From (1) and (2) we get
`60/sqrt(3) = (60 - "h")/(0.7813)`
60 × 0.7813 = `60 sqrt(3) = sqrt(3)`h
`sqrt(3)"h" = 60 sqrt(3) - 46.88`
= 60 × 1.732 – 46.88
= 103.92 – 46.88
1.732h = 57.04
⇒ h = `(57.04)/(1.732)`
h = `(570440)/(1732)`
= 32.93 m
∴ Height of the lamp post = 32.93 m
APPEARS IN
RELATED QUESTIONS
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
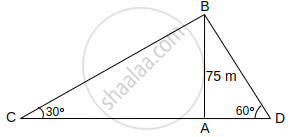
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
