Advertisements
Advertisements
प्रश्न
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
उत्तर
Let the height of the lamp post be h
The height of the tower (BC) = 60 m
∴ EC = 60 – h
Let AB be x
In the right ∆ABC,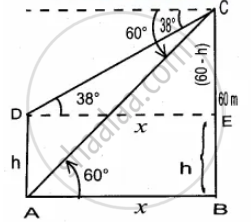
tan 60° = `"BC"/"AB"`
`sqrt(3) = 60/x`
x = `60/sqrt(3)` ...(1)
In the right ∆DEC, tan 38° = `"EC"/"DE"`
0.7813 = `(60 - "h")/x`
x = `(60 - "h")/(0.7813)` ...(2)
From (1) and (2) we get
`60/sqrt(3) = (60 - "h")/(0.7813)`
60 × 0.7813 = `60 sqrt(3) = sqrt(3)`h
`sqrt(3)"h" = 60 sqrt(3) - 46.88`
= 60 × 1.732 – 46.88
= 103.92 – 46.88
1.732h = 57.04
⇒ h = `(57.04)/(1.732)`
h = `(570440)/(1732)`
= 32.93 m
∴ Height of the lamp post = 32.93 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.