Advertisements
Advertisements
Question
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
Solution
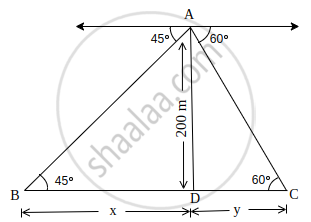
Let the aeroplane's position be A; B and C be two points on the two banks of a river such that the angles of depression at B and C are 45° and 60° respectively.
Let BD = x m, CD = y m
Given, AD = 200 m
In ΔADB, ∠D = 90°
tan 45° = `(AD)/(BD)`
⇒ 1 = `200/x`
⇒ x = 200 m ...(i)
In ΔADC, ∠D = 90°
tan 60° = `(AD)/(CD)`
⇒ `sqrt(3) = 200/y`
⇒ y = `200/sqrt(3)`
⇒ y = `(200sqrt(3))/3` ...(ii)
On adding equations (i) and (ii), we get
x + y = `200 + (200sqrt(3))/3`
= `(600 + 200sqrt(3))/3`
= `(200(3 + sqrt(3)))/3`
= `(200(3 + 1.732))/3`
= `(200 xx 4.732)/3`
= `946.4/3`
= 315.4 m
Hence, the width of the river is 315.4 m.
APPEARS IN
RELATED QUESTIONS
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
