Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
उत्तर
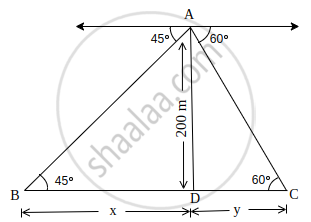
Let the aeroplane's position be A; B and C be two points on the two banks of a river such that the angles of depression at B and C are 45° and 60° respectively.
Let BD = x m, CD = y m
Given, AD = 200 m
In ΔADB, ∠D = 90°
tan 45° = `(AD)/(BD)`
⇒ 1 = `200/x`
⇒ x = 200 m ...(i)
In ΔADC, ∠D = 90°
tan 60° = `(AD)/(CD)`
⇒ `sqrt(3) = 200/y`
⇒ y = `200/sqrt(3)`
⇒ y = `(200sqrt(3))/3` ...(ii)
On adding equations (i) and (ii), we get
x + y = `200 + (200sqrt(3))/3`
= `(600 + 200sqrt(3))/3`
= `(200(3 + sqrt(3)))/3`
= `(200(3 + 1.732))/3`
= `(200 xx 4.732)/3`
= `946.4/3`
= 315.4 m
Hence, the width of the river is 315.4 m.
APPEARS IN
संबंधित प्रश्न
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground form the just observation point.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
The tops of two towers of height x and y, standing on level ground, subtend angles of 30º and 60º respectively at the centre of the line joining their feet, then find x : y.
In figure given ABCD is a rectangle, the value of CE is ____________.

A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
