Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
उत्तर
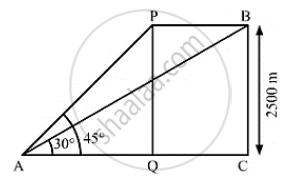
Let the height of flying of the aero-plane be PQ = BC and point A be the point of observation.
We have,
PQ = BC = 2500m, ∠PAQ = 45° and ∠BAC = 30°
In ΔPAQ,
` tan 45° = (PQ)/(AQ)`
`⇒ 1 = 2500/(AQ)`
`⇒AQ = 2500 m`
Also, in ΔABC,
`tan 30° = (BC)/(AC)`
`⇒1/ sqrt(3) = 2500/(AC)`
`⇒ AC = 2500 sqrt(3) m`
Now , QC = AC - AQ
`= 2500 sqrt(3)-2500`
`= 2500( sqrt(3)-1) m`
`= 2500 (1.732 - 1)`
`= 2500(0.732)`
`= 1830 m`
⇒ PB = QC = 1830
So, the speed of the aero-plane`(PB)/15`
`= 1830/15`
=122 m/s
`=122 xx3600/1000 km ⁄ h`
= 439.2 km /5
So, the speed of the aero-plane is 122m/ s or 439.2 km/ h.
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
In given figure, ABCD is a || gm. The length of AP is ____________.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
|
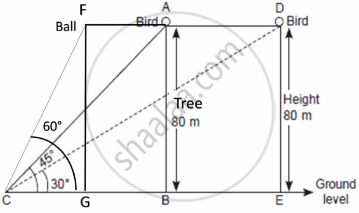
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?