Advertisements
Advertisements
Question
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
Options
\[3\sqrt{2}x\]
\[2\sqrt{3}x\]
\[\frac{\sqrt{3}}{2}x\]
\[\frac{2}{\sqrt{3}}x\]
Solution
Let h be the height of chimney AB

Given that: angle of elevation changes from angle `∠D=30°`to .`∠C=60°`
Then Distance becomes `CD=x` and we assume `BC=y`
Here, we have to find the height of chimeny.
So we use trigonometric ratios.
In a triangle,ABC
`⇒ tan C=(AB)/(BC)`
`⇒ tan 60°=(AB)/(BC)`
`⇒ sqrt3=h/y`
`⇒y=h/sqrt3`
Again in a triangle ABD,
`⇒ tan D=(AB)/(BC+CD)`
`⇒ tan 30°=h/(y+x)`
`⇒1/sqrt3=h/(y+x)`
`⇒sqrt3h=y+x`
`⇒sqrt3h=h/sqrt3+x` `["put" y=h/sqrt3]`
`⇒ h(sqrt3-1/sqrt3)=x`
`⇒h=x/(sqrt3-1/sqrt3)`
`⇒h=(sqrt3x)/2`
APPEARS IN
RELATED QUESTIONS
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
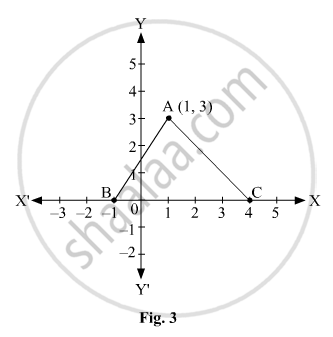
In Fig. 3, the area of triangle ABC (in sq. units) is:
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
In figure given ABCD is a rectangle, the value of CE is ____________.

A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
