Advertisements
Advertisements
Question
In Fig. 3, the area of triangle ABC (in sq. units) is:
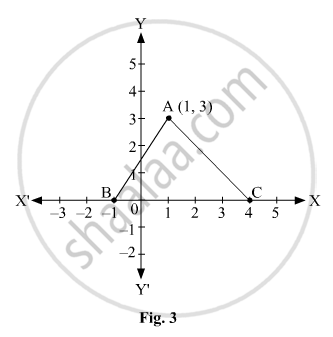
Options
(A) 15
(B) 10
(C) 7.5
(D) 2.5
Solution
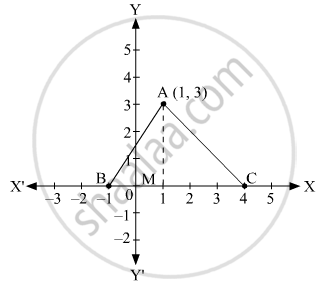
Construction: Draw AM ⊥ BC.
It can be observed from the given figure that BC = 5 unit and AM = 3 unit.
In ΔABC, BC is the base and AM is the height.
∴ Area of triangle ABC = `1/2xx`base x height
`=1/2xxBCxxAM`
`=1/2xx5xx3` sq.units
=7.5 sq.units
APPEARS IN
RELATED QUESTIONS
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
