Advertisements
Advertisements
Question
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
Solution
Let the height of the cell phone tower be h m
AD is the height of the apartment; AD = 50 m
Let AB be x
In the right triangle ABC
tan 60° = `"BC"/"AB"`
`sqrt(3) = "h"/x`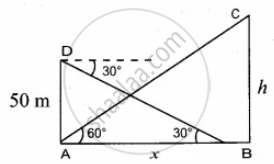
x = `"h"/sqrt(3)` ...(1)
In the right triangle ABD, tan 30° = `"AD"/"AB"`
`1/sqrt(3) = 50/x`
x = `50sqrt(3)` ...(2)
From (1) and (2) We get
`"h"/sqrt(3) = 50sqrt(3)`
h = `50sqrt(3) xx sqrt(3)`
= 50 × 3
= 150
Height of the cell phone tower is 150 m.
Yes, the cell phone tower meets the radiation norms.
APPEARS IN
RELATED QUESTIONS
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
