Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
उत्तर
C and D are the positions of the two boats.
Let the distance between the two boats be “x”
Let BC = y
∴ BD = (x + y)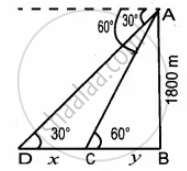
In the right ∆ABC, tan 30° = `"AB"/"BD"`
`1/sqrt(3) = 1800/(x + y)`
x + y = `1800sqrt(3)`
y = `1800sqrt(3) - x` ...(1)
In the right ∆ABC, tan 60° = `"AB"/"BC"`
`sqrt(3) = 1800/y`
y = `1800/sqrt(3)` ...(2)
From (1) and (2) we get
`1800/sqrt(3) = 1800sqrt(3) - x`
1800 = `1800 xx 3 - sqrt(3)x`
`sqrt(3)x` = 5400 – 1800
x = `3600/sqrt(3)`
= `(3600 xx sqrt3)/(sqrt3 xx sqrt(3)`
= `(3600 xx sqrt(3))/3`
= 1200 × 1.732
= 2078.4 m
Distance between the two boats = 2078.4 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
A flag-staff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flag-staff.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
