Advertisements
Advertisements
प्रश्न
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
उत्तर
Let h be the height of aeroplane p above the road.
And A and B be the two consecutive milestones, then AB = 1 mile. we have ∠PAQ = α and ∠PBQ = β.
We have to prove
`h = (tan alpha tan beta)/(tan alpha + tan beta)`
The corresponding figure is as follows
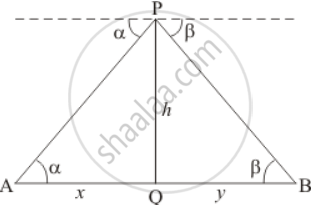
In ΔPAQ
`=> tan alpha = (PQ)/(AQ)`
`=> tan alpha = h/x`
`=> x = h/(tan alpha)`
`=> x = h cot alpha`
Again in ΔPBQ
`=> tan beta =(PQ)/(BQ)`
`=> tan beta = h/y`
`=> y = h/(tan beta)`
`=> y = h cot beta`
Now,
`=> AB = x + y`
`=> AB = h(cot alpha + cot beta)`
`=> AB = h(1/tan alpha + 1/tan beta)`
`=> AB = h((tan alpha + tan beta)/(tan alpha tan beta))`
Therefore `h = (tan alpha tan beta)/(tan alpha + tan beta)` (Since A B = 1)
Hence height of aero plane is `(tan alpha tan beta)/(tan alpha + tan beta)`
APPEARS IN
संबंधित प्रश्न
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
