Advertisements
Advertisements
Question
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
Solution
Let OX be the horizontal plane, AD be the tower and CD be the vertical flagpole
We have:
AB = 9m, ∠DBA= 30° and ∠CBA = 60°
Let:
AD = hm and CD = xm
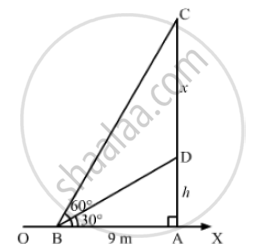
In the right ΔABD,we have:
`(AD)/(AB) = tan 30° = 1/ sqrt(3)`
`⇒ h/8 = 1/sqrt(3)`
`⇒ h = 9/sqrt(3) = 5.19 `m
Now, in the right ΔABC,we have
`(AC)/(BA) = tan 60° = sqrt(3)`
`⇒ (h+x ) /9 = sqrt(3)`
`⇒ h + x = 9 sqrt(3)`
By putting h= `9/sqrt(3)` in the above equation, we get:
`9/sqrt(3) + x = 9 sqrt(3) `
`⇒ x = 9 sqrt(3) - 9/ sqrt(3) `
`⇒ x = (27-9)/ sqrt(3) = 18/ sqrt(3) = 18/ 1.73 = 10.4`
Thus, we have:
Height of the flagpole = 10. 4 m
Height of the tower = 5. 19 m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
