Advertisements
Advertisements
Question
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
Solution
Solution:
Let AB is the tower of height h meter and AC is flagstaff of height x meter.
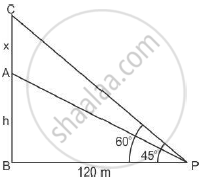
∠APB=45° and ∠BPC =60°
`Tan 60 = (x+h)/120`
`sqrt3=(x+h)/120`
`x=120sqrt3-h`
`tan 45=h/120`
therefore height of the flagstaff =
`=120sqrt3-120`
`=120(sqrt3-1)`
`=120 xx73`
`=87.6 cm`
APPEARS IN
RELATED QUESTIONS
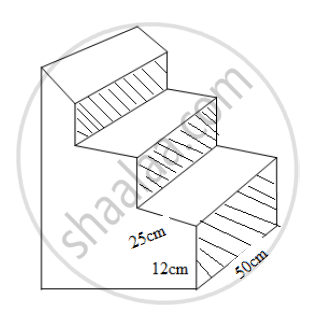
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
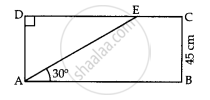
In given figure, the value of AE is ____________.
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
